 2SC1775は、高いhFE値を持ったたいへんすぐれたオーディオ用低雑音トランジスタです。
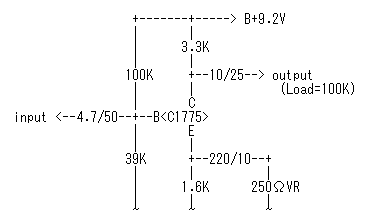
2SC1775は、高いhFE値を持ったたいへんすぐれたオーディオ用低雑音トランジスタです。実験回路は右図のとおりです。電源電圧は9.2V、コレクタ電流は約1.07mAで、エミッタ側に可変抵抗器を挿入して電流帰還量を可変できるようにしました。
コレクタ負荷抵抗値は3.3KΩですが、後続の回路が100KΩの入力インピーダンスで受けていますので実際の負荷抵抗値は約3.2KΩとなります。
トランジスタを使用した増幅回路を設計する場合、電流・電圧の配分や動作条件、増幅率等は簡単に計算で求まりますが、どのくらい歪むかについてはなかなか検証できません。そこで、ごく簡単な1段増幅回路を組み立ててこの回路では一体どのくらいの歪み率特性が得られるのかを検証してみることにしました。休日のちょっとした時間つぶし程度の実験ですので、体系だった実験ではありませんが、それでも結構使えるデータが得られました。
2SC1775は、高いhFE値を持ったたいへんすぐれたオーディオ用低雑音トランジスタです。
実験回路は右図のとおりです。電源電圧は9.2V、コレクタ電流は約1.07mAで、エミッタ側に可変抵抗器を挿入して電流帰還量を可変できるようにしました。
コレクタ負荷抵抗値は3.3KΩですが、後続の回路が100KΩの入力インピーダンスで受けていますので実際の負荷抵抗値は約3.2KΩとなります。
エミッタ側の可変抵抗器の値を、0〜200Ωの間で変化させて測定しました。実際は、エミッタ側のバイアス用抵抗(1.6KΩ)との並列合成値になりますからエミッタ側電流帰還抵抗値は0〜178Ωとなります。エミッタ側の可変抵抗が0Ωの時の利得の実測値が135倍ですから、2SC1775のre=3.2kΩ÷135=23.7Ωということになります。ちなみに、トランジスタ増幅回路における増幅率は、コレクタ負荷抵抗とここで求めたreによって以下の式で求めることができます。利得=コレクタ負荷抵抗÷reそして、reの値はほぼコレクタ電流に反比例し、それはre=26(定数)÷コレクタ電流値という関係にあります。試しに、上式のコレクタ電流値に1.07mAを代入してみると、re=26(定数)÷1.07mA=24.3Ωになりますから、実測による推定値23.7Ωにかなり近い値です。さて、エミッタ側の可変抵抗が30Ωの時の利得は計算上30Ωの時の利得=3.2kΩ÷(29.4Ω+23.7Ω)=60.3倍が求まりますが、これは実測値60.6倍と良く一致します。
可変抵抗値 1.6kΩとの合成値 エミッタ抵抗値 利得(計算値) 利得(実測値) 0Ω 0Ω 24.3Ω ×131.7 ×135 30Ω 29.4Ω 53.7Ω ×60.3 ×60.6 100Ω 94Ω 118.3Ω ×27.05 ×27.6 200Ω 178Ω 202.3Ω ×14.8 ×16.0
歪み率は1kHzで測定しました。
電流帰還ゼロ(エミッタ側の可変抵抗が0Ω)の時では、0.1V出力時でさえ何と0.9%もの歪みがあり、1V出力時では7%にも達します。
エミッタ側の可変抵抗が100Ωの時では、利得が約1/5になっており約14dBの電流帰還がかかっていることになりますが、この時の歪み率は電流帰還ゼロの場合のほぼ1/5(0.1V出力時で0.19%、1V出力時で1.6%)にまで改善されています。
真空管増幅回路では一般に1V出力時で0.05〜0.3%くらいですからそれにくらべるとかなりひどい数字で、このままの状態ではプリ・アンプの出力段に使用するわけにはゆかないでしょう。
しかし、歪み率はコレクタ負荷抵抗の値におおむね反比例するという癖がありますから、実験回路の3.3kΩをその3倍の10kΩ、10倍の33kΩとすることで大幅な改善が期待でき、ほぼ、真空管増幅回路並の歪み率特性にまで追いこむことが可能です。
トランジスタ増幅回路では、コレクタ側の負荷抵抗を大きくしてゆくにつれて歪み率はどんどん低くなってゆきます。動作条件と信号レベルさえ適切であればトランジスタ回路でも充分低歪みの増幅が可能です。また、コレクタ側の負荷抵抗値が低くても、コレクタ電流が多ければやはり歪み率を低くできます。どちらの場合でも、電源電圧は高くなります。トランジスタでは、真空管と比較すると非常に低い電源電圧でも効率の良い動作をさせることができますが、低い動作電圧の領域で低歪み動作は望めないので設計に注意が必要です。
 データライブラリに戻る
データライブラリに戻る