負帰還のメカニズム
前章で、負帰還とは「入力信号と出力信号とを比較(引き算)し、比較した結果を入力・合成する」ものだと書きました。これを図にすると以下のようになります。
増幅回路に入力された信号は、出力側から増幅されて出てきますが、出力の一部(あるいはほとんど全部)を入力側に戻してやります。どれくらい、どういう風に戻すかは途中に挿入された「負帰還素子」によって決定されます。さて、戻された出力信号は入力信号と比較され、合成されて再び増幅されて出力側に現われます。
増幅回路のなかで歪みが生じていると、出力側からは歪んだ波形が現われます。歪んだ波形の一部が帰還されるわけですが、まだ歪んでいない入力波形と歪んだ波形とが比較され、引き算の結果である差分によって入力波形が矯正されたらどうなるでしょうか。入力波形は、オリジナルとは違った波形となってしまいますが、これが再び増幅回路を通ることにより、もういちど歪みが与えられてしまいます。しかし、今度は、歪んだことによって元の入力波形に戻ってしまうのではないでしょうか。
実際には、信号はこのように単純にぐるぐる回るわけではありません。入力側に信号がはいり、これが増幅されて出力側に現われた瞬間、その出力信号は直ちに帰還され、あっという間に入力信号が矯正されてしまいます。一瞬のできごとなのです。
逆に、矯正されないで増長されてしまう場合もあります。これを正帰還といいます。正帰還の場合は、出力信号が帰還されて入力信号を増長し、これが増幅されて再び帰還され、さらに増長・・・これが繰り返されるため、増幅回路は発振してしまいます。引き算を行っているのが負帰還、足し算を行っているのが正帰還です。
では、負帰還では発振しないかというとそうともいえません。増幅回路は普通、非常に低い周波数と非常に高い周波数ではゲインが低下するとともに、その副産物として位相が回転します。位相が回転してしまうと、負帰還のつもりが正帰還のような状態に近づいてゆくため、発振しそうでしない不安定な状態になったり、あるいは簡単に発振してしまったりもします。このへんのことは、後の章で具体的に説明したいと思います。
負帰還では、帰還された信号によって入力信号が食われてしまうために、入力された信号が目減りしたようなことになります。帰還して引き算した分だけみかけのゲインが低下するのです。また、負帰還の効果を十分発揮させるには、それなりの帰還量を確保しなければなりません。従って、負帰還を前提に増幅回路を設計する場合は、どれくらいの負帰還を施すのかを検討した上で、増幅回路全体のゲインを余分にとっておかなければなりません。
2段増幅回路における負帰還
第15章「電圧増幅回路の設計と計算その1 (2段コンデンサ結合増幅回路)」では、以下のような2段電圧増幅回路について設計をしたのを覚えていらっしゃるでしょう(忘れてしまっていたらもういちど思い出してください)。この回路を借用して、負帰還の原理について考えてみることにします。
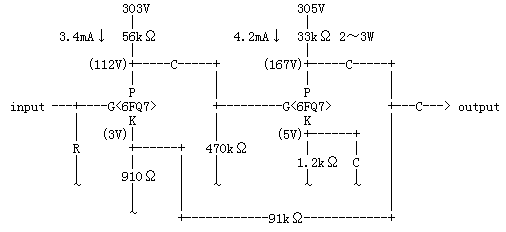
その前に、この2段電圧増幅回路のゲインを計算しておきましょう。
初段管内部抵抗 = 11kΩ + ( 0.91kΩ × 23 ) = 31.9kΩ
初段負荷抵抗 = ( 56kΩ × 470kΩ ) / ( 56kΩ + 470kΩ ) = 51kΩ
初段ゲイン = 22 × 51kΩ / ( 31.9kΩ + 51kΩ ) = 13.5倍
次段管内部抵抗 = 11kΩ
次段負荷抵抗 = ( 33kΩ × 91.91kΩ ) / ( 33kΩ + 91.91kΩ ) = 24.2kΩ
次段ゲイン = 22 × 24.3kΩ / ( 11kΩ + 24.3kΩ ) = 15.1倍
総合ゲイン = 13.5倍 × 15.1倍 = 203.9倍
次段の計算で注意しなければならないのは、負帰還素子の91kΩと910Ωが負荷に並列にはいる、ということです。負帰還素子も負荷となりますので、負帰還素子のインピーダンス値を小さな値とする場合は、次段の負荷として重過ぎないように配慮しなければなりません。
本題その1・・・方程式で解く
では、この増幅回路に1(mV)の交流信号を入力してみます。そして、出力側にx(mV)の信号が得られたとします。この信号は、91kΩと910Ωで減衰させられて101分の1の0.0099x(mV)の信号となって初段カソードにかかります。グリッド1(mV)、カソードが0.0099x(mV)ですから、グリッド-カソード間には1-0.0099x(mV)の信号が与えられることになります。これが203.9倍されて、出力側がきっかりx(mV)になればつじつまが合います。
この様子を式にすると以下のようになります。
x = ( 1 - 0.0099x ) × 203.9倍
ごく単純な一次関数ですね。これを解くと、
x = 67.55倍
と出ます。これが、負帰還のかかったアンプの最終ゲインになるのです。
ちょっと検証してみましょう。見かけのゲインが67.55倍ですから、出力側には67.55mVの信号が現われています。これが帰還素子によって101分の1に減衰させられて0.6688mVになり、これが初段カソードにかかります。入力信号電圧は1mVでしたから、引き算された0.3312mVがグリッド-カソード間にかかります。これを203.9倍してみますと、0.3312mV × 203.9倍 = 67.53mV(計算誤差が出ます)となり、ちゃんとつじつまが合いました。負帰還のかかった増幅回路では、この状態で安定します。

本題その2・・・算数で解く
さて、今度は同じことを、算数で解いてみたいと思います。方程式で解く場合は、入力を1とおきましたが、算数で解く場合は、出力を1000とおきます。出力が1000(mV)ですから、負帰還素子によって初段カソードに帰還される信号電圧は、1000mV × 1/101 = 9.901mV
となり、また、増幅回路の利得は203.9倍ですから、1000(mV)の出力を得るための増幅回路の正味の入力電圧は、
1000mV ÷ 203.9倍 = 4.904mV
となります。inputのところに入力された信号電圧のうち、帰還された分(9.901mV)は差っ引かれますから、inputに必要な信号電圧は、
9.901mV + 4.904mV = 14.805mV
でなければなりません。従って、この増幅回路の負帰還を含めた全体の利得は、
1000mV ÷ 14.805mV = 67.54倍
となって、方程式で解いた結果と一致します。その様子を以下の図にまとめました。(わずかに計算誤差が生じていますが、ご了解ください。)

このように、負帰還時の利得は、算数で簡単に解くことができます。むしろ、算数で解いた方が、負帰還のメカニズムが良く理解でき、間違いも起こしにくいのです。方程式を使ってしまうと、負帰還のメカニズムはともかく、式さえ解けば答えが得られてしまうため、考え方にちょっとした勘違いが生じても自分でその間違いに気づくことができません。
「入力を1」とおいて式を立てて「x」の値を求めるのが方程式を使った解き方、「出力を1000」とおいて逆に戻りながら解いてゆくのが算数を使った解き方です。
負帰還時の増幅回路の挙動については、算数で解く方法さえ身につけていれば、オーバーオール帰還だけでなく、それがカソード帰還であろうと、P-G帰還であろうと、超3結回路であろうと、あっさりと解けてしまうのです。
増幅回路のゲインそのものは変化しない
重要なのは、増幅回路のゲインそのものは相変わらず203.9倍なのであって、これが変化したのではないということです。入力信号と帰還信号との引き算が起こったことによって、見かけ上のゲインが67.55倍になっただけなのです。(世間には、負帰還のかかった増幅回路では、初段、次段それぞれのゲインが変化する、などという珍説も見受けられますが、とんでもない話です。)こうしてみると、負帰還がかかった状態であっても、増幅回路自体の基本動作は無帰還の時となにひとつ変わってはいないことに気づきます。そして、増幅回路の各段の前後で一体どのくらいの信号レベルになっているのかは、簡単に求めることができます。実験回路では、次段のゲインは15.1倍でしたから、出力電圧67.55mVの時の「初段-次段の中間」では、67.55mV÷15.1=4.47mVになっているわけです。
こういうしくみを理解していれば、いかなるタイプの負帰還もこわくなくなります。自分で解析できるようになるからです。
さて、おさらいです。私の場合、帰還後のゲインは以下のような式で計算しております。
帰還後のゲイン = ( 元のゲイン × 帰還定数 ) / ( 元のゲイン + 帰還定数 )
です。ところで、上式でいう帰還定数というのは、帰還素子の減衰率の逆数(なんていうとややこしく思うでしょうけれど)、要するに
帰還定数 = ( 91kΩ + 910Ω ) / 910Ω = 101倍
のことです。これは、私流の計算方法なので、帰還定数の考え方も私流です、あしからず。(一般に知られる負帰還の計算法では、帰還定数βはこの逆数を使いますが、式が複雑になって暗算できないので、私はあえてこの方法を使っています。)
元のゲインが十分大きくて、帰還定数がちいさい場合は、帰還後のゲインは限りなく帰還定数に近づいてゆきます。反対に、元のゲインは大きくなくて、帰還定数が非常に大きい場合は、帰還後のゲインは限りなく元のゲインを同じになってゆきます。そして、元のゲインと帰還定数が全く同じ場合は、帰還後のゲインは両方のちょうど半分になります。このあたりの事情がわかってくると、負帰還の塩梅や計算はほとんどそらでできるようになります。
