負帰還方法の種類
真空管・半導体を問わず、あらゆる回路において負帰還技術は応用されています。負帰還のかけ方には非反転増幅回路と反転増幅回路の2種類があります。OPアンプのつなぎ方にもにも2種類ありますが、負帰還の仕組みは全く同じです。ここでは、特に真空管増幅回路に的を絞って例を挙げていますが、計算法は半導体もOPアンプも同じです。文系でも無理なくわかるように、難しい数式は一切使わずに解説します。
非反転（P-K）帰還
2段増幅回路の2段目プレートあるいはスピーカー出力から初段カソードに帰還する方法です。負帰還ループの入力と出力で位相が同じ（反転しない）回路の負帰還のかけ方です。アンプのほとんどは非反転増幅回路です。３２．負帰還その１（メカニズム）では以下のような2段増幅回路を例に負帰還のメカニズムについて説明しましたが、この回路は典型的なP-K帰還にあたります。
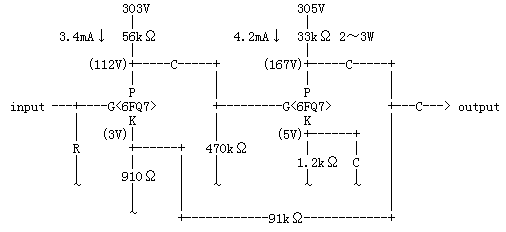
＜利得の計算＞
負帰還利得の計算では、その回路が「何倍になろうとしているのか」を考えるとわかりやすいです。負帰還とは、入力と出力の関係を常に一定（＝なろうとする利得）に保とうとする作用です。利得だけでなく波形も相似形を保とうとするから歪みが減るのです。全ての帯域で利得を同じにしようとするから周波数特性が良くなるのです。
上の図の場合は91kΩと910Ωですから
なろうとする利得＝1＋（負帰還抵抗÷カソード抵抗）＝1＋（91kΩ÷910Ω）＝101倍
裸利得が203.9倍だとすると101倍にはなれなくて67倍程度になります。計算では調和平均を使います。裸利得が101倍と203.9倍と10000倍のケースを比較してみます。
帰還利得＝（裸利得×なろうとする利得）÷（裸利得＋なろうとする利得）
裸利得101倍の時＝（101×101）÷（101＋101）＝50.5倍・・・負帰還量＝6dB（2倍）
裸利得203.9倍の時＝（203.9×101）÷（203.9＋101）＝67.5倍・・・負帰還量＝9.6dB（3.02倍）
裸利得10000倍の時＝（10000×101）÷（10000＋101）＝100倍・・・負帰還量＝40dB（100倍）
裸利得が十分大きくて、なろうとする利得がちいさい場合は、負帰還はたっぷりとかかって帰還後の利得は限りなくなろうとする利得に近づいてゆきます。反対に、裸利得は大きくなくて、なろうとする利得が非常に大きい場合は、負帰還量は少なく帰還後の利得は限りなく裸利得を同じになってゆきます。そして、裸利得となろうとする利得が全く同じ場合は、帰還後の利得は両方のちょうど半分になります。このあたりの事情がわかってくると、負帰還の塩梅や計算はほとんどそらでできるようになります。
反転（P-G）帰還
真空管1段増幅のプレートからグリッドに帰還する方法です。この方法では、歪みが減少し、出力インピーダンスも下がりますが、一方で入力インピーダンスがかなり低くなってしまうのが欠点です。入力インピーダンスは、入力に直列に挿入されている抵抗値+アルファになります。この欠点を承知の上でP-G帰還を採用した例として有名なのが、LUX製のSQ38FDです。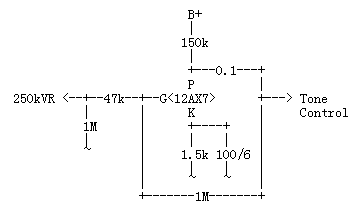
LUX製SQ38FD（ラインアンプ部）LUXの初代SQ38では、ラインアンプ部は12AU7を無帰還で使用していました。SQ38FDになった時、12AU7を12AX7に変更し、P-G帰還をかけることで高すぎる12AX7のゲインを殺し（12AU7はちょうど良かった）、高すぎる12AX7の出力インピーダンスを12AU7以下に下げてます。ここまでならば12AU7のままで良かったわけですが、P-G帰還のおかげで歪みを大幅に下げることができています。
こまかいことを言わせてもらうと、250kΩのボリューム・コントロールの位置によって信号源インピーダンスが変化するので、実質的な帰還抵抗値は（ここに掲載した回路図での計算上）47kΩ〜105.8kΩの範囲で変化します。すなわち、ボリューム・コントロールの位置によって負帰還量が変化してしまっているのです。結構、綱渡り的な設計だなぁと思う反面、そういう事情はアンプを使う側には全く見えないわけで、うまい設計だとも思います。SQ38FDの回路についての考察はここにあります。
＜入力インピーダンスの計算＞
ところで、p-g帰還の増幅回路の入力インピーダンスはどうやって計算したらいいかですが、これが意外に簡単で、以下の式で求まります・・でも、何故どの記事にもどの本にも書かれていないのでしょう？この値をちゃんと計算しようとした人はいないのかもしれません。
入力インピーダンス = 入力抵抗＋｛帰還抵抗÷（裸利得＋1）｝
なぜそうなるか。下の図をみてください。
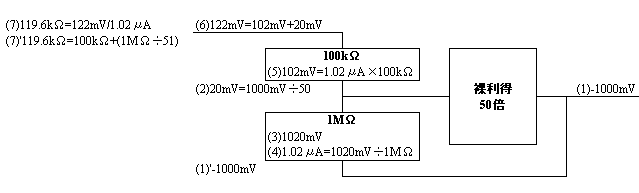
入力抵抗100kΩ、帰還抵抗1MΩで裸利得50倍のp-g帰還回路があるとします。
（1）（1）' 何らかの信号を入力して出力側に1000mVの信号が現われたとします。-1000mVとなっているのは、プレート側出力の位相はグリッド入力と反対だからです。
（2）裸利得は50倍でしたから、グリッド入力は、1000mV÷50＝20mVであるはずです。
（3）1MΩの抵抗の両端にかかる電圧は、20mV＋1000mV＝1020mVですから、
（4）1MΩに流れる電流は、1020mV÷1MΩ＝1.02μAです。
（5）同じ電流が100kΩにも流れますから、100kΩの両端の電圧は、1.02μA×100kΩ＝102mV。
（6）従って、そもそも入力された電圧は、102mV＋20mV＝122mVだったことになれば辻褄が合います。
（7）負帰還後の利得は、1000mV÷122mV＝8.2倍です。
（8）そこでオームの法則（R＝E/I）に従って計算すると、122mV÷1.02μA＝119.6kΩが求まるというわけです。
（9）この式を代入・変形を繰り返してゆくと最終的に「100kΩ＋｛1MΩ÷（50＋1）｝＝119.6kΩ」になるのです。
＜利得の計算＞
反転帰還の利得の計算は少し複雑です。反転帰還では、入力信号経路に抵抗が割り込んでいるためにこれによるロス（減衰）があります。計算は、二段階に分けて行います。
- 裸利得となろうとする利得による帰還利得の計算・・・非反転増幅回路と同じ
- 減衰の計算・・・普通のアッテネータと同じ
なろうとする利得＝1＋（負帰還抵抗÷グリッド抵抗）＝1＋（1MΩ÷100kΩ）＝11倍
裸利得が50倍だとすると11倍にはなれなくて9倍程度になります。計算では調和平均を使います。裸利得が11倍と50倍と100000倍のケースを比較してみます。
帰還利得＝（裸利得×なろうとする利得）÷（裸利得＋なろうとする利得）
裸利得11倍の時＝（11×11）÷（11＋11）＝5.5倍
裸利得50倍の時＝（50×11）÷（50＋11）＝9.02倍
裸利得10000倍の時＝（10000×11）÷（10000＋11）＝10.99倍
裸利得となろうとする利得が同じ時は、負帰還利得はその半分になります。そして裸利得がなろうとする利得よりも十分に大きいほど負帰還利得はなろうとする利得に近づいてゆきます。
100kΩと1MΩによるアッテネータがあるのと同じと思ってください。減衰率の分は負帰還に貢献していないので負帰還量は目減りします。
減衰率＝帰還抵抗÷（入力抵抗＋帰還抵抗）＝1MΩ÷（100kΩ＋1MΩ）＝0.909倍
反転帰還利得＝帰還利得×減衰率
裸利得11倍の時＝5倍・・・負帰還量＝6dB（1.99倍）
裸利得50倍の時＝8.2倍・・・負帰還量＝14.9dB（5.54倍）
裸利得10000倍の時＝9.989倍・・・負帰還量＝59.2dB（910倍）
カソード帰還
メインアンプの出力段に局部帰還をかけると、出力管の出力インピーダンスを下げたのと同じ効果を得ることができます。しかし、出力管にP-G帰還をかけると、出力段の入力インピーダンスが下がってしまうために、ドライバ段の負荷が重くなってしまい、却って設計が難しくなってしまいます。加えてグリッドに入力抵抗が割り込むために、グリッド電流が少しでも流れるとドライブできなくなります。そこで、出力トランスの2次側から出力管のカソードに負帰還をかける方法が考案されました。これを一般にカソード帰還と呼びます。「EL34３結シングル・アンプその２」では、このカソード帰還を使っています。普通の回路であれば、図中のX点はアースされるはずですが、これが出力トランスの2次側に接続されています。カソード帰還では、負帰還量を制御するための抵抗がありません。
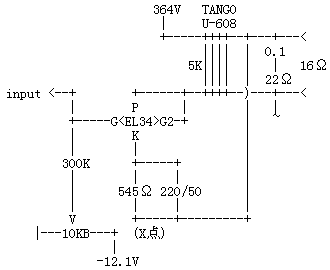EL34３結シングル・アンプその２より
カソード帰還における帰還量は、出力トランスの2次側で発生する信号電圧と、出力管のグリッドに入力される信号電圧の2つの比によって求めます。たとえば、「EL34３結シングル・アンプその２」の最大出力が5Wであるとすると、出力トランスの2次側16Ωタップでの出力電圧は、
平方根（5W×16Ω）＝8.95V
となり、最大出力時の出力管グリッドの入力信号電圧は、バイアス電圧（約35V）のルート2分の1とみなせますから、
35÷1.414＝25V
になります。この2つの数字を使って帰還量を求めると、
（8.95V＋25V）/25V＝1.358倍＝3dB弱
と求まります。わずかな負帰還量ですが、これでEL34（3結）単独で3程度であったダンピング・ファクタを4.4まで改善できます。もしこれが、6V6のビーム管接続であったならば、6V6オリジナルのダンピング・ファクタ（たった0.1）が一挙に1.2まで改善されてしまいます。
出力側から初段カソードへの帰還
真空管アンプにおけるもっともオーソドックスな帰還方法が、これではないかと思います（下図）。本章の冒頭で解説した非反転帰還です。一般に、出力トランスの2次側(またはNFB専用巻線)から、初段カソードに帰還させます。こうすることで、アンプ全体の特性を一挙に改善しようというわけです。
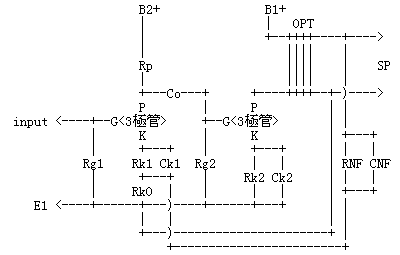
帰還定数は、RNFとRk0の比で決定されます。初段管の内部抵抗を低くして高域特性とドライブ能力を高めるために、初段カソードは抵抗1本で済ますことをせず、Rk1とRk0とに分けて、Ck1を抱かせる工夫をすることが多くみられます。こうすることで、初段の利得の目減りも防ぐことができます。こうすることでヒーターハムも減らすことができます。
問題は、出力トランスの1次側と2次側の位相関係です。負帰還回路では、位相が逆転していると正帰還になってしまい、即座に発振します。よく、出来上がったメインアンプの電源をONにした途端に、スピーカからけたたましく「ギャー！」という音が出ることがありますがこれが正帰還です。日本駄球協会では、これを「産声」と呼んでいます。さて、正帰還になってしまったら、出力トランスの1次側または2次側の接続を反対に繋ぎ替えてやります。この位相関係は、ドライバの段数が1段増えるごとに反対になりますから、1段ドライブのアンプを2段ドライブに改造した場合は要注意です。
負帰還抵抗（RNF）は、よくコンデンサ（CNF）を抱いていることがあります。このコンデンサは、負帰還時の超高域での位相回転を抑制して、動作を安定させる働きがあります。方法としては、100kHz以上の周波数特性や波形の崩れと相談しながら、コンデンサ容量を決定してゆきます。このような操作のことを「位相補正」といい、負帰還回路ではつきものです。この方法による位相補正で手に余る場合は、負帰還量を減らすか、アンプ自体の高域特性を故意に悪くするという方法が取られました。
かつては、「電圧増幅段の高域特性を故意に悪くする」という方法が一般的でしたが、最近では、これをやるとアンプの中高域の音の品位を損ねるというので、逆に「電圧増幅段の高域特性を極端に良くする（・・・そういうことができる時代になったのです）」という方法に変化しつつあります。古典アンプの名機達にはなかった発想です。
出力側から差動初段グリッドへの帰還
マイケルソン・オースチンのTVA1アンプを筆頭に、初段を差動回路で構成するアンプがひとつの流れを作り始めています。それは、位相反転精度が非常に高いということ、理論的に2次歪みが発生しないということが主なる理由です。初段を差動回路とした場合、その一方のグリッドに信号を入力しますが、負帰還は残った側のグリッドに戻します。以下の回路は、初段を真空管ではなくFETを使用していますが、基本は真空管の場合と全く同じで、負帰還は出力トランス2次側から初段FETのゲートにかけられています。
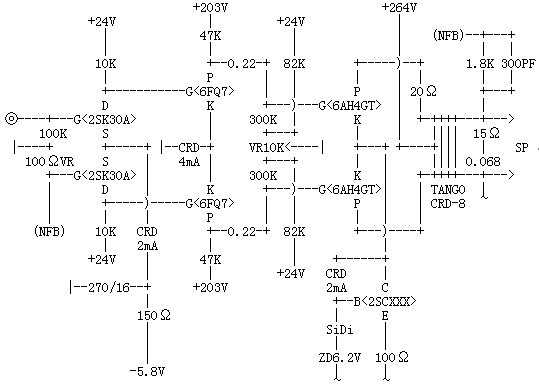
帰還定数を決定する帰還抵抗のうち、受け側は100Ωの可変抵抗器になっており、この可変抵抗器を0Ωとした場合は無帰還アンプとなります。そして抵抗値を増やしてゆくにつれて、帰還量は徐々に増加してゆきます。この方法は非常に便利で、そのアンプにとって最適な任意の負帰還量を自在に設定できます。
負帰還抵抗1.8kΩには、300pFの位相補正コンデンサを抱かせており、この位相補正は200kHzあたりから効きはじめ、290kHzで-3dBのレスポンス低下の定数設定になっています。また、出力トランスの2次側に、抵抗とコンデンサの直列回路（15Ω＋0.068μF）が挿入されています。これは、超高域でのスピーカを含む負荷系全体のインピーダンスが高くなりすぎるのを補正するためのもので、これがあるのとないのとでは、アンプの超高域での安定度に大きな差が出ます。どちらの回路も、負帰還をかけたアンプの安定度を確保する重要な働きがあります。
